答：这个问题的标准答案，就是用角动量守恒来解释，前面李永乐老师，已经给出了完整且专业的回答。

在这，我换一个方式给大家解释其中原理。

角动量这个概念，比较抽象，没有能量守恒和动量守恒那样直观，导致部分人不太喜欢角动量这个概念，包括我自己也是的。

那么陀螺不倒，可以不用角动量，只用牛顿力学的基本概念来解释吗?

答案是肯定的，我们就来分析分析，对于高速旋转的陀螺。

一、我们先来分析不倒的原因

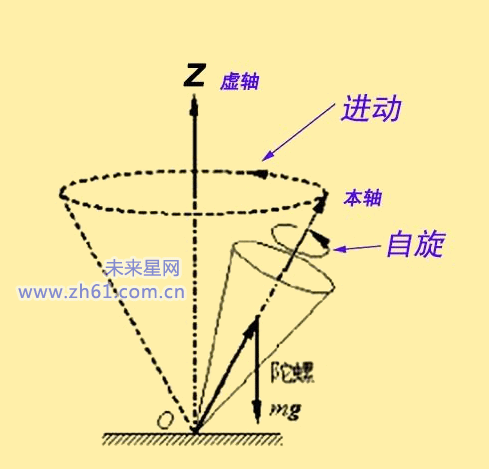
取A、B两质点分析，它们绕着陀螺的本轴旋转，设该旋转角速度为w1，v1=w1*r1，称为自旋；还绕着垂直的虚轴旋转，设该旋转角速度为w2，v2=w2*r2，称作叫做进动。

所以A、B两点的运动，是两者的合成，我们分开分析：

1、对于A点

合成速度va=v1+V2，需要注意的是，计算本轴提供的向心力，使用的速度是va，而不是v1；

2、对于B点

合成速度vb=v1-V2，计算本轴提供的向心力，使用的速度是vb，而不是v2；

因为旋转半径都是r，所以很容易得出，本轴为自旋提供的向心力有：Fa>Fb；

根据作用力与反作用力的关系，那么A、B两质点，对本轴的反作用力就是：Fa’>Fb’；

正是这个差异，使得陀螺整体受到一个回到站立方向的力；很容易发现，自旋速度越大，这个差异越大，那么陀螺越不容易倒。

二、补充进动

上面直接给出进动，在这里，我们可以用同样的方式，去分析进动的原理。

当陀螺完全垂直时，受到重力作用有倾倒的倾向，一旦陀螺发生倾倒，那么对于C、D两质点的速度，也可以用上面的技巧分析。

结果是C、D两点离心力的差异，使得陀螺受到一个向D方向的力，正是这个力，使得陀螺产生进动。

于是，我们就可以总结啦！

高速旋转的陀螺：

重力使得陀螺倾倒

一但倾倒，就让陀螺有了进动的倾向

一旦发生进动，进动使自旋对本轴的离心力产生差异

然后该差异，又使得陀螺倾向于站立

这就是陀螺不到的原因，该解释未用到角动量的概念，大家是否更容易理解呢？

因为这个现象是旋转物体的通有属性，于是物理学上发明了一个“角动量”，用来描述高速旋转物体保持平衡的能力。

好啦！我的答案就到这里，喜欢我们答案的读者朋友，记得点击关注我们！