第15 章积分
积分是个很强大的工具, 可以用来求不规则图形的面积, 不规则物体的体积, 以及变速运动物体的路程.
15.1 求和符号
下面和氏的每一项都是平方数的倒数, 并且有希腊字母 "Σ"(sigma) 便捷的表达方式:
如果想要用求和符号表示下面的表达式需要仔细考虑, 将 j 代入校验:
15.1.1 一个有用的求和
同一个求和用求和符号来表达会有很多种方法, 下面三种表示等价:
15.1.2 伸缩求和法
上面这个求和中可以消掉很多相同的项, 这种类型的级数叫伸缩级数. 可以把它合并成更简单的形式:
例如:
实际上求和的结果是下面的形式:
另一方面, (j2-(j-1)2)(j2-(j-1)2) 化简后就是 2j-1 , 所以也就证明了.
仔细考虑这个求和, 会发现左边仅仅是前n 个奇数的和. 例如当n = 5 时, 左边是1+3+5+7+9, 这个和是25. 这就是 5252.
也可以推导出下面两个有用的公式:
15.2 位移和面积
下面考虑这个问题: 如果知道一辆汽车在某一时段内每一时刻的行驶速度, 那么它在这个时间段内的总位移是多少呢?
15.2.1 三个简单的例子
考虑三辆车沿着一条笔直的高速公路向前行驶. 每一辆车都是在下午3 点钟开始行驶, 下午5 点钟结束旅行. 并且不考虑加速的时间.
第一辆车匀速行驶, 在整个时间段内的平均速率为50 英里/小时. 所以在3点到5点 [3, 5] 这个时间段内的速率为 v(t) = 50 . 利用路程= 平均速率 x 时间得到结果.
也就是下面这辆车所走的路程就是速度对时间的图像的面积 50 x 2 = 100.
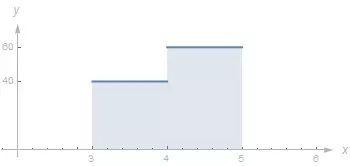
第二辆车, 它在第一个小时的速度为40 英里/小时; 从4 点钟开始它以60 英里/小时的速度行驶, 看下面的图形:
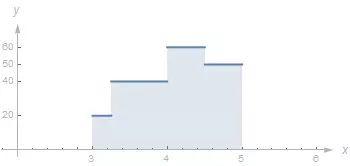
第三辆车在开始15 分钟的速率为20 英里/小时, 接下来一直到4 点钟的速率为40 英里/小时. 在4 点钟的时候, 它提速到60 英里/小时, 该速率保持了半个小时. 在最后的半个小时中, 它的速率降为50 英里/小时.
从这个图像中可以看出, 可以通过把这2 个小时的时间段分成4 个小时间段去计算出它所走的路程.通过图像可以看出, 共有4 个长方形, 计算其面积求和既是第三辆车所走的路程.
15.2.2 一段更常规的旅行
假设时间段为[a, b], 并且也假设这个时间段可以分成 n 个时间段, 从而保证汽车在每个小的时间段内是匀速行驶的. 那么总的位移公式为:
15.2.4 连续的速度
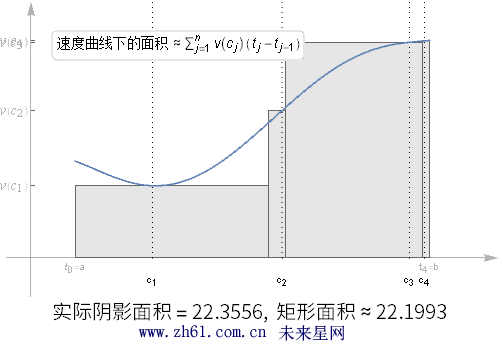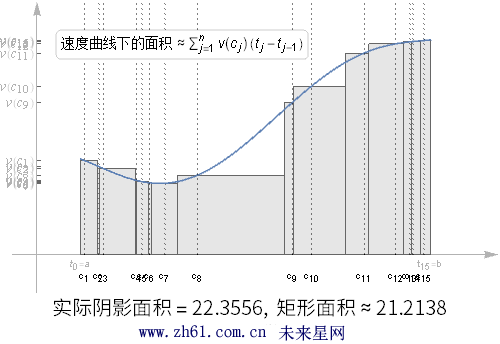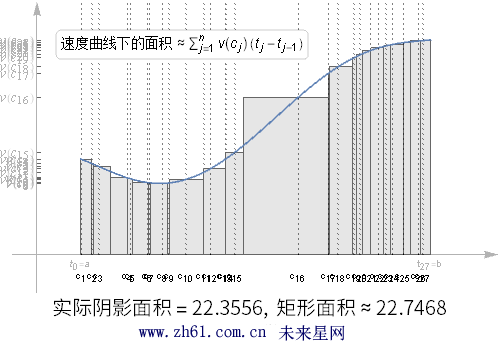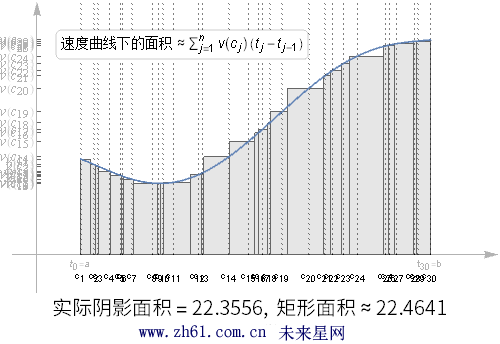
现在考虑速度为时间 t 的连续函数, 在整个[a, b] 区间内重复这个划分的过程, 在每个时间段内, 我们都取个样本速度.
观察上动图随着划分区间增大, 阴影部分的面积比之前的分区更接近于真实面积了, 但是如果其中的某个分区很大, 对估算结果仍然会有很大的影响.
如果这些分区的最大值趋于 0 , 那么这个估算的结果就越来越精确了, 就得到了下面的公式:
因为最大区间趋于0, 这样划分的数目就会越来越大, 所以上述极限自动包含了n 趋于∞ 这样一个思想.
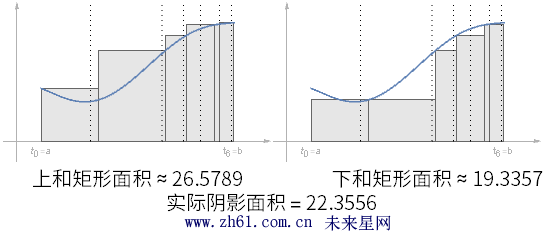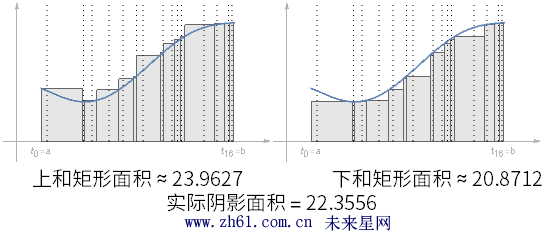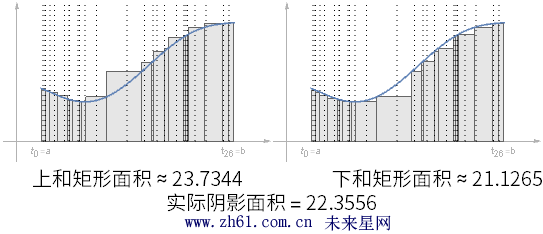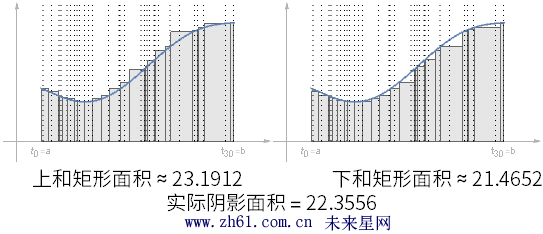
15.2.5 两个特别的估算
如果在不同的划分中选择函数的最大值和最小值, 所形成的矩形当然会不同
通过对这两种情况的分析, 可以得到下和<= 曲线下的实际面积<=上和.
当最大区间趋于0 时, 三明治定理(夹挤定理)可以证明这两个求和都趋于实际的正确面积.(本章完)
「予人玫瑰, 手留余香」
转发既是支持和帮助, 感谢感谢!

 更多
更多
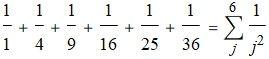

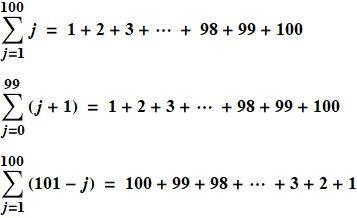
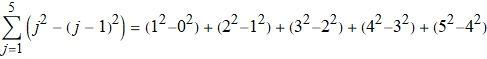
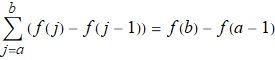
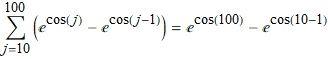
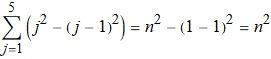
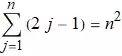
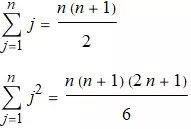

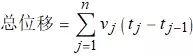

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底