第11 章导数和图像(The Derivative and Graphs)

本章要介绍以下知识点：

(1) 函数的局部和全局极值问题, 以及怎样用导数去找极值;

(2) 罗尔定理和中值定理, 以及它们对绘制函数图像的意义;

(3) 二阶导数的图像阐释;

(4) 对导数为零点的分类.

11.1 函数的极值(Extrema of Functions)

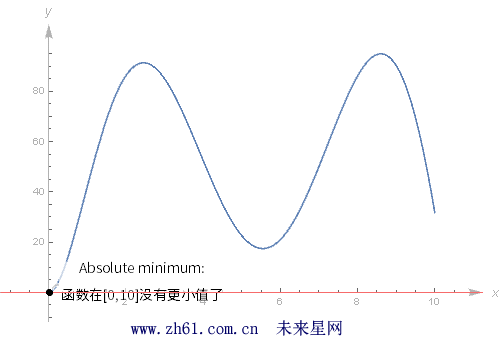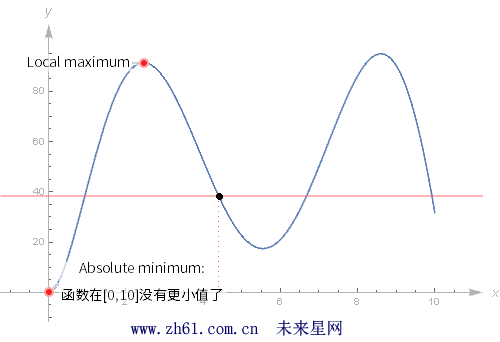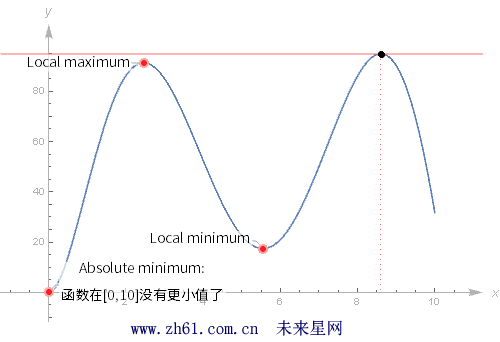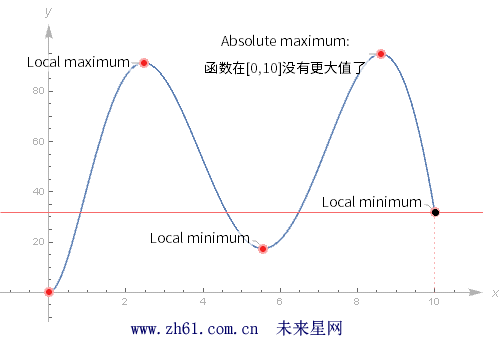
如果 x = a 是函数 f 的一个极值点, 这就意味着函数 f 在a 点处有最大值或最小值, 不过这里还有区分两种极值: 全局极值和局部极值(global and local).

注: 全局极值和局部极值或称绝对极大值 Absolute maximum(minimum)和局部极值Local maximum(minimum).

11.1.1 全局极值和局部极值

每一个全局最大值都是局部最大值.

11.1.2 极值定理(The Extreme Value Theorem)

在第 5 章中, 我们看到过最大值与最小值定理(Max-Min Theorem): 连续函数在一个闭区间 [a, b] 内一定有一个全局最大值和一个全局最小值.

如果函数在 x = c 处的导数为零或导数不存在, 我们就称 x = c 为临界点(critical point), 又称驻点(Stationary Point). 值得注意的是, 一个函数的驻点不一定是这个函数的极值点(考虑到这一点左右一阶导数符号不改变的情况); 反过来, 在某设定区域内, 一个函数的极值点也不一定是这个函数的驻点(考虑到边界条件), 马上就再看到这一点.

极值定理(Extreme Value Theorem)假设函数 f 定义在开区间 (a, b) 内, 并且点c 在 (a,b) 区间内. 如果点 c 为函数的局部最大值或最小值, 那么点c 一定为该函数的临界点. 也就是说, f'(c) = 0 或 f'(c) 不存在.

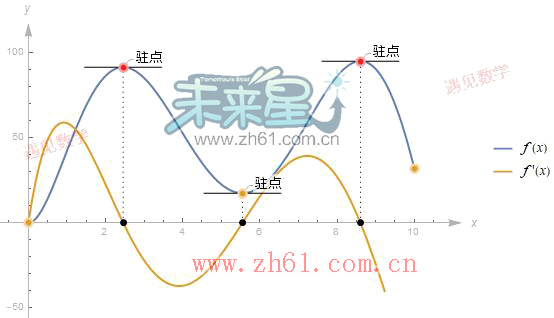
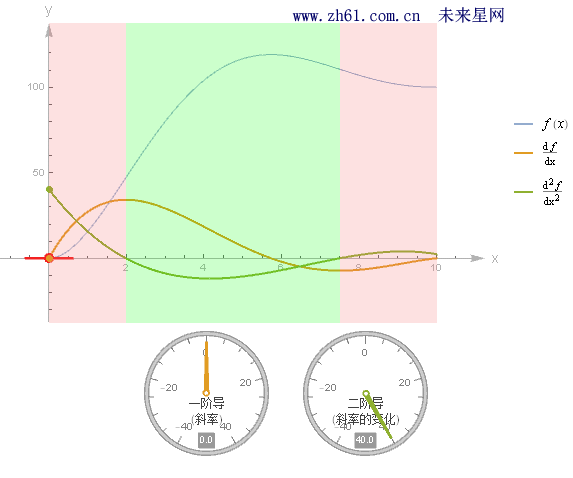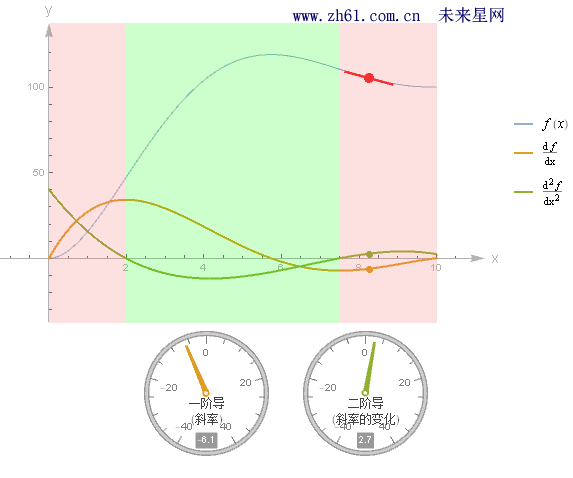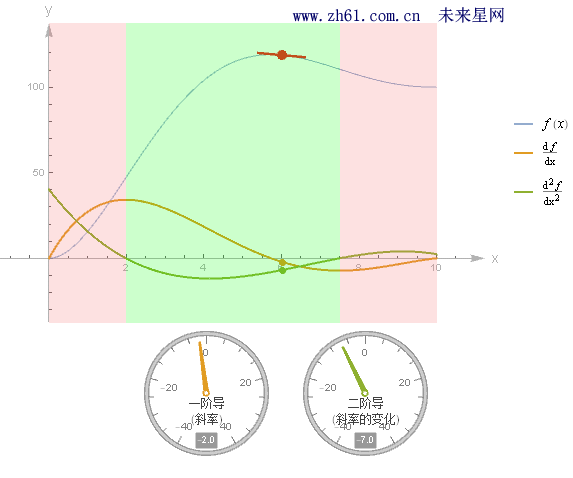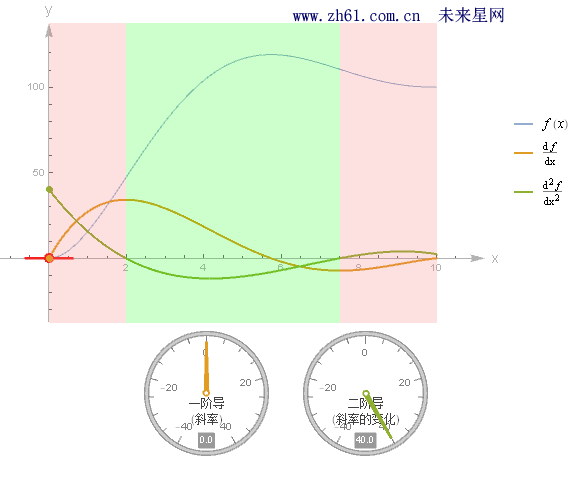
例如来看 f'(c) = 0 图形示例, 观察上图黄橙色一阶导函数与 x 轴相交的黑点部分.

11.1.3 求全局最大值和最小值

11.2 罗尔定理

罗尔定理(Rolle's Theorem)假设函数 f 在闭区间 [a,b] 内连续, 在开区间 (a, b) 内可导. 如果 f(a) = f(b); 那么在开区间 (a,b) 内至少存在一点 c, 使得 f'(c) = 0.

11.3 中值定理(Mean Value Theorem)

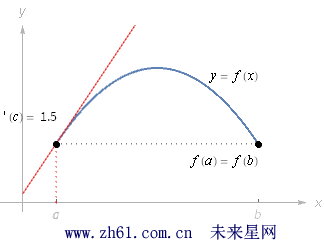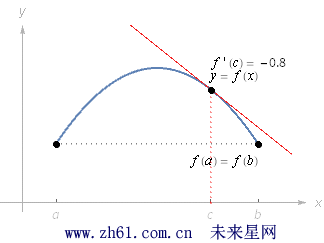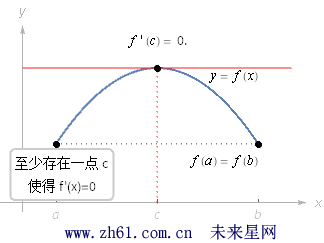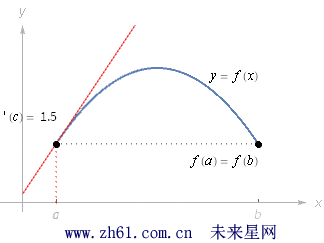
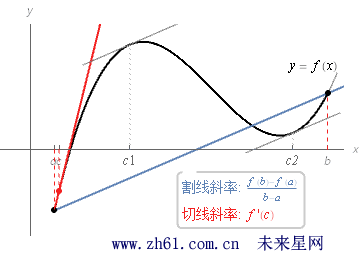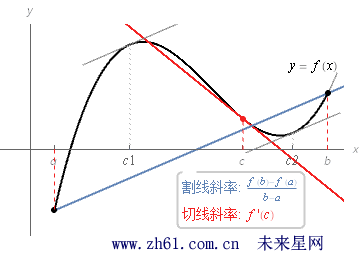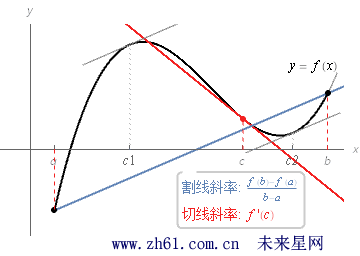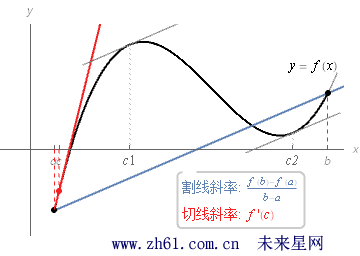
中值定理:假设函数 f 在闭区间 [a,b] 内连续, 在开区间 (a,b) 内可导, 那么在开区间 (a,b) 内至少有一点 c 使得 f(b)−f(a)b−a=f'(c)f(b)−f(a)b−a=f'(c).

中值定理和罗尔定理这两个定理的条件几乎是相同的. 在两个定理中, 函数f 都要求在闭区间 [a,b] 内连续, 在开区间 (a,b) 内可导. 但罗尔定理还要求 f(a) = f(b), 中值定理则没要求这一点.

11.4 二阶导数和图像

如果把二阶导数看作导数的导数, 那么可以把二阶导数写为 (f')'(x) > 0. 这意味着导函数 f'(x) 始终是增函数.

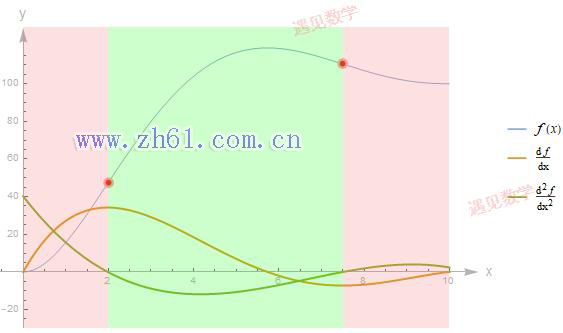
观察下面图中不同的 (0,2) 与 (7.5, 10)范围二阶导数 f''(x) > 0 (凹向上, 如碗型: 凸函数Convex function), 所以导函数 f'(x) 始终是增函数;而在 (2,7.5) 区间二阶导数 f''(x) < 0(凹向下: 凹函数Concave function), 所以导函数 f'(x) 始终是减函数.

注: 国内凹凸函数有些书定义是相反的.

原函数凹凸性改变的地方,称之为拐点(inflection point), 也是上图区域颜色改变之处(用红点标识出来的地方).

关于拐点的更多说明

如 果 x = c 点是函数 f 的拐点, 则有 f''(c) = 0.

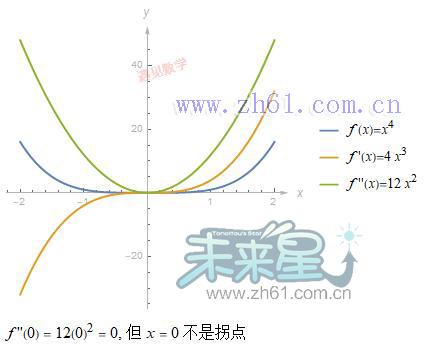
如果 f''(c) = 0, 则 c 点不一定都是函数 f 的拐点, 看下面反例的图形:

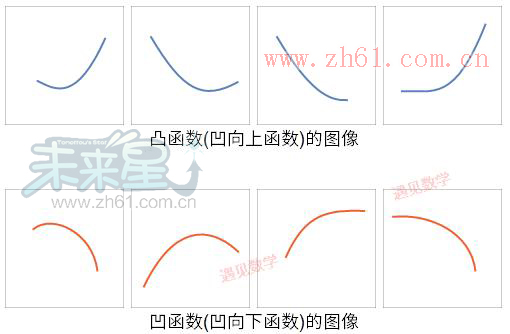
凸函数(凹向上函数)图像:

11.5 对导数为零点的分类

假设有一个函数 f 以及数c 使得 f'(c) = 0. 除了可以确定地说 c 点是函数 f 的临界点. 也就是 x=c 有三种可能:

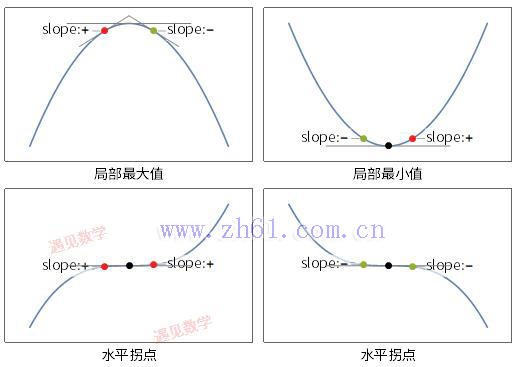
1. 局部最大值

2. 局部最小值

3. 水平拐点

在这三种情况下, 切线都是水平的. 如果只计算出 f'(c)=0 , 判别的方法有两种:

1. 用一阶导数, 然后计算 x=c 左右两侧一阶导数的正负符号

2. 用二阶导数, 考虑在 x=c 点的二阶导数的符号.

11.5.1 使用一次导数

假设 f'(c) = 0, 这时有：

• 如果从左往右通过 c 点 f'(x) 的符号由正变负, 那么c 点为局部最大值;

• 如果从左往右通过 c 点, f'(x) 的符号由负变正, 那么c 点为局部最小值;

• 如果从左往右通过 c 点, f'(x) 的符号不发生变化, 那么c 点为水平拐点.

11.5.2 使用二阶导数

再来看一下当f'(c) = 0 时几种常见可能性:

• 如果 f''(c) < 0, 那么x = c 为局部最大值;

• 如果 f''(c) > 0, 那么x = c 为局部最小值;

• 如果 f''(c) = 0, 那么无法判断发生了什么! 还需要使用上面一阶导数方法再做判别;

(本章完)

「予人玫瑰, 手留余香」

转发既是支持帮助[遇见数学]更快发展, 非常感谢!

所用书籍《普林斯顿微积分读本》